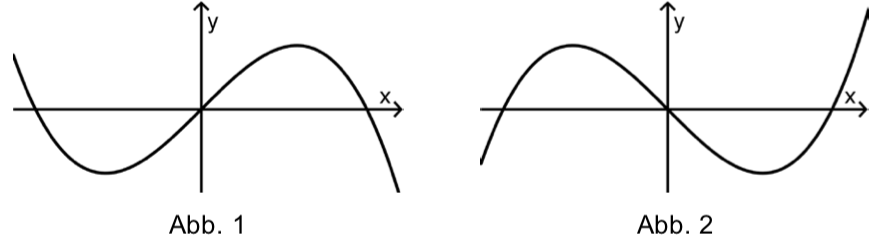Analysis, Teil A, Aufgabengruppe 2

Die Aufgabe verlangt Verständnis für die Bedeutung des Scharparameters einer ganzrationalen Funktionenschar 3. Grades.

Teilaufgabe 4a

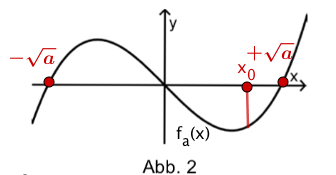
Abbildung 2 zeigt einen Graphen aus der Funktionenschar $f_a$.

Begründung:

Das Verhalten einer ganzrationalen Funktion für $x\to \pm \infty$ wird bestimmt durch das Vorzeichen des Faktors beim Glied mit dem höchsten Exponenten.

Da $a\in {ℝ}^{+}$ ist $\frac{1}{a}>0$ und es gilt: $${\displaystyle \underset{x\mapsto +\infty }{\lim }{f}_a(x)=+\infty }$$.

Alternative Begründung ohne Grenzwertbetrachtung:

$f_a(x)$ läßt sich in Linearfaktoren zerlegen:

$$f_a(x)={\displaystyle \frac{1}{a}{x}^3-x=\frac{1}{a}\cdot x\cdot (x^2-a)=\frac{1}{a}\cdot x\cdot (x-\sqrt{a})(x+\sqrt{a})}$$

Beachte die Benutzung der 2. binomischen Formel für $x^2-a=x^2-(\sqrt{a}{)}^2$.

Teilaufgabe 4b

Notwendige Bedingung, dass $x=3$ ein Extremum ergibt: $f_a^{\prime }(3)=0$.

$$\begin{array}{lcll}& & & \text{Differenziere}{f}_a(x)\\ f_a^{\prime }(x)& =& {\displaystyle \frac{3}{a}{x}^2-1}& \text{Setze für}x\text{den Wert 3 ein.}\\ f_a^{\prime }(3)& =& {\displaystyle \frac{27}{a}-1}& \text{Setze}{f}_a^{\prime }(3)=0\\ {\displaystyle \frac{27}{a}-1}& =& 0& |\cdot a\text{(Gleichung für a!)}\\ 27-a& =& 0& \\ a& =& 27& \end{array}$$

Nachweis, dass $a=27$ für $x=3$ tatsächlich ein Extremum ergibt:

$$\begin{array}{lcll}& & & \text{Differenziere}{f}_a^{\prime }(x)\\ f_a^{\prime \prime }(x)& =& {\displaystyle \frac{6}{a}\cdot x}& \text{Setze}a=27\text{ein}.\\ f_{27}^{\prime \prime }(x)& =& {\displaystyle \frac{6}{27}\cdot x}& \text{Setze}x=3.\\ f_{27}^{\prime \prime }(3)& =& {\displaystyle \frac{2}{3}>0}& \Rightarrow x=3\text{ergibt für}{f}_{27}\text{ein lokales Minimum}.\end{array}$$